浮游海蝴蝶（planktonic sea butterfly）中流场，速度场检测方案(粒子图像测速)

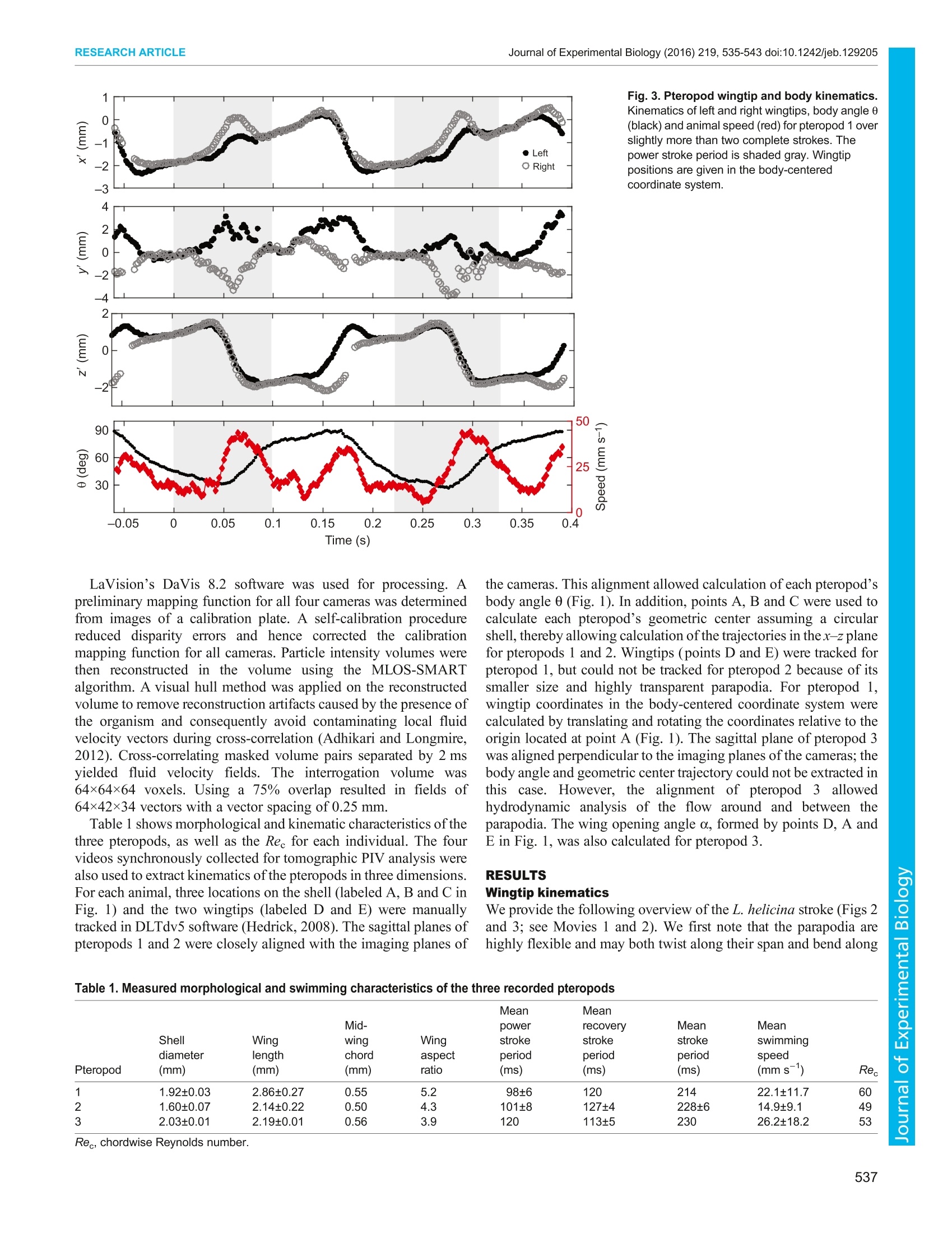
C 2016. Published by The Company of Biologists Ltd Journal of Experimental Biology (2016) 219，535-543 doi：10.1242/jeb.129205 RESEARCH ARTICLEJournal of Experimental Biology (2016) 219，535-543 doi：10.1242/jeb.129205 Underwater flight by the planktonic sea butterfly David W. Murphy1，*，+， Deepak Adhikari1， Donald R. Webster and Jeannette Yen² In a remarkable example of convergent evolution， we show that thezooplanktonic sea butterfly Limacina helicina ‘flies'underwater in thesame way that very small insects fly in the air. Both sea butterflies andflying insects stroke their wings in a characteristic figure-of-eightpattern to produce lift， and both generate extra lift by peeling theirwings apart at the beginning of the power stroke (the well-knownWeis-Fogh‘clap-and-fling'mechanism). It is highly surprising to find azooplankter ‘mimicking'insect flight as almost all zooplankton swim inthis intermediate Reynolds number range (Re=10-100) by using theirappendages as paddles rather than wings. The sea butterfly is alsounique in that it accomplishes its insect-like figure-of-eight wing strokeby extreme rotation of its body (what we call ‘hyper-pitching')， aparadigm that has implications for micro aerial vehicle (MAV) design.No otheranimal， to our knowledge， pitches to this extent under normallocomotion. KEY WORDS： Pteropods， Zooplankton， Swimming， Weis-Foghmechanism， Insect flight， Convergent evolution INTRODUCTION Zooplankton swim to find food and mates and to escape from andavoid predators. Indeed， in what is likely the largest animal migrationon Earth in terms of biomass， many zooplankton species swimhundreds of meters to the water surface every night to graze andavoid predation (Hays， 2003). How these millimeter-to-centimeterscale organisms efficiently propel themselves at intermediateReynolds numbers is thus of great interest. Zooplankton and smallinsects swim and fly， respectively， in an intermediate Reynoldsnumber regime (Re=ul/v=10-1000， where u is the characteristicvelocity scale， I is the characteristic length scale and v is kinematicviscosity) in which both viscous and inertial forces are important.However， they generally use different locomotion techniques. Mostzooplankton species (e.g. copepods and euphausiids) in this Reregime paddle through the water with drag-based propulsion inwhich viscous drag on a hairy， jointed appendage is maximizedduring the power stroke and minimized on the recovery stroke(Strickler， 1975； Yen， 2000；Kiorboe et al.，2014). In contrast， insectssuch as fruit flies use their wings as airfoils to generate aerodynamiclift (and drag) on both power and recovery strokes (Dickinson et al.，1999). Insects may generate additional lift via unsteady aerodynamicinteractions between the wings such as the well-known Weis-Foghclap-and-fling’mechanism (Weis-Fogh， 1973； Lighthill， 1973；Ellington， 1984a，b； Dickinson et al.， 1999). ( School o f Civil and Environmental Engineering， Georgia Institute of Technology， A tlanta， GA 30332-0355， USA. S c hool of Biology， Georgia Institute of Technology， ) ( Atlanta ， GA 30332-0230， USA.*Present address： Department o f Mechanical Engineering， The Johns HopkinsUniversity， Baltimore ， MD 21218-2681， USA. ) ( + Author for correspondence (dwmurphy@jhu.edu) ) The Weis-Fogh mechanism， including variants such as the‘partial clap-and-fling'，‘near clap-and-fling'and ‘clap-and-peel'， isused by a wide variety of flying insect species (Ellington， 1984a).The technique was first noted in the tiny wasp Encarsia formosa(Weis-Fogh， 1973)， which hovers by beating its sub-millimeter-length wings at a frequency of approximately 400 Hz. Use of theWeis-Fogh mechanism appears to be an obligate behavior for smallinsects flying at less than about Re=100， including thrips (Ellington，1984a； Santhanakrishnan et al.， 2014)， the greenhouse white-flyTrialeurodes vaoparium (Weis-Fogh， 1975) and the parasitoid waspspecies Muscidifurax raptor and Nasonia vitripennis (Miller andPeskin， 2009). For the slightly larger Drosophila species， flying atRe>100， the Weis-Fogh mechanism is rarely used in free flight but isseen when the animal is tethered (Vogel， 1967； Lehmann et al.，2005). Larger flying insects， such as moths and butterflies(Ellington， 1984a) and locusts in climbing flight (Cooter andBaker， 1977)， have also been observed using the Weis-Foghmechanism. Experimental measurements of the flow generated bythe Weis-Fogh mechanism in freely flying insects have provenprohibitive because of the small time and length scales involved，though studies of tethered insects (Dickinson and Gotz， 1996；Fuchiwaki et al.， 2013) and dynamically scaled models (Dickinsonet al.， 1999； Lehmann et al.， 2005； Lehmann and Pick， 2007) haveoffered valuable insight. Computational modeling has also provenhelpful for understanding the fluid dynamics of flight by tiny flyinginsects (Miller and Peskin， 2005，2009； Santhanakrishnan et al.，2014； Jones et al.， 2015). It has been suggested， based on kinematics measurements， thatmarine mollusks such as Clione limacina (Satterlie et al.， 1985；Szymik and Satterlie，2011)， Clione antarctica (Borrell et al.，2005)and Limacina helicina (Chang and Yen， 2012) also performa version of the clap-and-fling at a similar intermediate Re.These marine organisms potentially offer the opportunity toexperimentally measure flows induced by a freely ‘flying’animalusing the Weis-Fogh mechanism because of the larger sizes of thesemollusks and their lower appendage beat frequencies (comparedwith tiny flying insects). Furthermore， the appendage kinematicsand body pitching of these larger organisms beating at lowerfrequencies could be resolved with much greater detail. Limacinahelicina locomotion was investigated in the current study. The zooplankter L. helicina is a pelagic thecosomatous sea snailknown as the sea butterfly. Limacina helicina is ecologicallyimportant for the large biomass it maintains in polar pelagicecosystems. Furthermore， because its shell sinks when the animaldies， L. helicina is geochemically important as a major conduit ofcarbon to the deep ocean (Bednarsek et al.， 2012). In temperateregions， L. helicina reaches shell diameters of 1-4 mm and swims atspeeds of 10-50 mm s-， whereas in the sub-Arctic， their shells maygrow to 14 mm， with swimming speeds reaching 120 mm s-(Chang and Yen， 2012). In contrast to many other zooplankton，pelagic pteropods such as L. helicina (see Figs 1 and 2； Movies 1and.22)) possess smooth. wing-like： swimmingappendages(parapodia)that flap inaa complex three-dimensionalstroke pattern resembling the wingbeat kinematics of flying insects (Changand Yen， 2012). Indeed， the chordwise Reynolds number (Re) ofL. helicina swimming (Rec=40-90) lies between the Re of flight bythrips (Ree=5-35) (Weis-Fogh， 1973； Santhanakrishnan et al.，2014) and fruit flies (Re=100-300) (Dickinson et al.， 1999). Thesesimilarities suggest that， like insect flight， pteropod swimming alsomay be lift based and raise the possibility that pteropods may haveconverged to the same lift generation mechanisms used by manyinsects (e.g. the Weis-Fogh clap-and-fling). This convergencewould have occurred along a completely different evolutionarylineage as Insecta and Gastropoda are thought to have diverged 550million years ago (Valentine， 1997； McGhee， 2011). Lift-basedflapping locomotion is well known among larger aquatic animals，such as sea turtles， but would be highly unusual for aquatic animalson the scale of zooplankton (at low Re)， where the ratio of lift-to-drag on a flapping appendage decreases dramatically. The potentialbenefit to pteropods， however， is that flapping appendages are moremechanically efficient than rowing appendages at all swimmingspeeds (Walker and Westneat， 2000). In addition， flapping strokesgenerategreater verticalilforceatattttheReynoldsnumberscharacteristic of pteropod swimming (Jones et al.， 2015). Efficientgeneration of lift is particularly important to L. helicina as itpossesses a dense aragonite shell which causes it to rapidly sinkwhen not swimming or suspended from its parachute-like mucusfeeding web (Gilmer and Harbison， 1986； Bednarsek et al.， 2012；Chang and Yen， 2012). Our hypothesis is that， despite living in a low Re aquaticenvironment， this pteropod employ；s lift-based locomotiontechniques similar to those used by many small， flying insects. Inorder to determine whether pteropod swimming is employing lift-ordrag-based propulsion， we filmed free-swimming individuals ofL. helicina in the laboratory to obtain highly resolved three- Fig. 1. Pteropod morphology and coordinate systems. Schematic diagramof a pteropod showing the global (xyz) and body-centered (x'y'z') coordinatesystems， the locations of the tracked points (A-E) and definition of the bodyangle 0. Fig. 2. Pteropod wing stroke. Sequence of inverted-color particle imagevelocimetry (PIV) images for pteropod 1 (left) and pteropod 3 (right) illustratingthe stroke cycle. t is time normalized by the stroke period. The scale barrepresents 1 mm. One wing in each image is outlined in red. dimensional flow fields surrounding the pteropod. We measuredthree-dimensional kinematics of the pteropod body and wingtipsfrom the same recordings. This is the first study to measure detailedkinematics and the flow fields created by a freely ‘flying’organismusing the Weis-Fogh mechanism and provides the most completepicture to date of how the clap-and-fling is used in free ‘flight’. MATERIALS AND METHODS Limacina helicina (Phipps 1774) were collected off the coast nearthe Hadfield Marine Station in Newport， OR， USA， in June 2011and were shipped overnight to Atlanta， GA， USA， where they werekept in buckets of artificial seawater at 32 ppt in an environmentalchamber set at 12°C. Tomographic particle image velocimetry (PIV)measurements of freely swimming animals were collected at500 frames s- within 1 week using the four-camera systemdescribed by Murphy et al. (2012，2013). The flow was seeded with11.7 um mean diameter hollow glass spheres and illumination wasprovided by near-infrared lasers (808 nm). The pteropods generallyswam vertically upwards until they reached the water surface， atwhich point they sank to the bottom and began swimming upwardsagain. Three recordings in which an animal entered the illuminated16×10.5×8.5 mm measurement volume were suitable for processingand further analysis (designated as pteropods 1， 2 and 3). LaVision’s DaVis 8.2 software was used for processing. Apreliminary mapping function for all four cameras was determinedfrom images of a calibration plate. A self-calibration procedurereduced disparity errors and hence corrected the calibrationmapping function for all cameras. Particle intensity volumes werethen reconstructed in the volume using the MLOS-SMARTs1algorithm. A visual hull method was applied on the reconstructedvolume to remove reconstruction artifacts caused by the presence ofthe organism and consequently avoid contaminating local fluidvelocity vectors during cross-correlation (Adhikari and Longmire，2012). Cross-correlating masked volume pairs separated by 2 msyielded fluid velocity fields. The interrogation volume was64x64×64 voxels. Using a 75% overlap resulted in fields of64×42×34 vectors with a vector spacing of 0.25 mm. Table 1 shows morphological and kinematic characteristics ofthethree pteropods， as well as the Re for each individual. The fourvideos synchronously collected for tomographic PIV analysis werealso used to extract kinematics of the pteropods in three dimensions.For each animal， three locations on the shell (labeled A， B and C inFig. 1) and the two wingtips (labeled D and E) were manuallytracked in DLTdv5 software (Hedrick， 2008). The sagittal planes ofpteropods 1 and 2 were closely aligned with the imaging planes of the cameras.This alignment allowed calculation of each pteropod’sbody angle 0 (Fig.1). In addition， points A， B and C were used tocalculate each pteropod’s geometric center assuming a circularshell， thereby allowing calculation of the trajectories in the x-z planefor pteropods 1 and 2. Wingtips (points D and E) were tracked forpteropod 1， but could not be tracked for pteropod 2 because of itssmaller size and highly transparent parapodia. For pteropod 1，wingtip coordinates in the body-centered coordinate system werecalculated by translating and rotating the coordinates relative to theorigin located at point A (Fig. 1). The sagittal plane of pteropod 3was aligned perpendicular to the imaging planes of the cameras； thebody angle and geometric center trajectory could not be extracted inthis case. However， the alignment of pteropod 3 allowedhydrodynamic analysis of the flow around and between theparapodia. The wing opening angle a， formed by points D， A andE in Fig. 1， was also calculated for pteropod 3. RESULTS Wingtip kinematics We provide the following overview of the L. helicina stroke (Figs 2and 3； see Movies 1 and2). We first note that the parapodia arehighly flexible and may both twist along their span and bend along Table 1. Measured morphological and swimming characteristics of the three recorded pteropods Mean Mean Mid- power recovery Mean Mean Shell Wing wing Wing stroke stroke stroke swimming diameter length chord aspect period period period speed Pteropod (mm) (mm) (mm) ratio (ms) (ms) (ms) (mm s ) Re 1 1.92±0.03 2.86±0.27 0.55 5.2 98±6 120 214 22.1±11.7 60 2 1.60±0.07 2.14±0.22 0.50 4.3 101±8 127±4 228±6 14.9±9.1 49 3 2.03±0.01 2.19±0.01 0.56 3.9 120 113±5 230 26.2±18.2 53 Fig. 4. Pteropod swimming trajectories. Upward swimming trajectories ofpteropods 1-3. Points indicate the geometric center of the shell for pteropods 1and 2 and the average of shell points B and C for pteropod 3. their chord throughout the complex stroke (Chang and Yen， 2012).The pteropod begins its power stroke with its wings raised togetherabove its shell. The tips of the arching wings touch but are separatedat the wing base， forming a canopy. The wingtips roll along eachother and separate from the leading edge to the trailing edge，twisting along their span as they begin the power stroke. The wingsstroke diagonally downwards， ending the power stroke by lyingacross the shell. The wingtips extend beyond the shell and bend inthe spanwise direction to approach or touch each other. Much of thisspanwise bending， which occurs at the extreme positions (i.e. the Fig. 5. Transformation of pteropod wingtip coordinates by hyper-pitching. Sagittal view of wingtip coordinates for pteropod 1 in body-centered(top) and global (bottom) coordinate systems. Fig. 6. Flow measurements of Weis-Fogh ‘near-fling'maneuver by thepteropod. Sequence of flow measurements in a plane bisecting a Limacinahelicina specimen that is performing a Weis-Fogh near-fling. Color contoursrepresent the x-component of vorticity. Vectors， which lie tangent in the plane，indicate flow direction and magnitude. Pairs of oppositely signed vortices oneither side of the animal (marked with black arrows at t'=0.06) result from theprevious stroke. beginning and end of the power stroke)， appears to occur in thenarrow， proximal half ofthe wing； the broad， distal wingtips appearrelatively flat throughout the stroke. The power stroke induces a 50-60 deg rotation of the pteropod about its transverse axis and a rapidincrease in its speed to approximately 40 mm s-. In preparation forthe recovery stroke， the pteropod then slides its wings upwardsalong its body as its speed decreases to about 10 mm s-. In therecovery stroke， the pteropod strokes51its wings diagonallydownwards in the opposite direction， again increasing theanimal's speed (to about 35 mm s-) and pitching the pteropod inthe opposite direction. Finally， the pteropod recovers its wings totheir original position above the shell. The pteropod gains elevationduring both power and recovery strokes， resulting in an upwardsawtooth trajectory (see Fig. 4) as it beats it wings at a frequency of5-9 Hz (Chang and Yen， 2012). After accounting for the extreme rotation of L. helicina， its wingkinematics show striking similarity to those of insects flying in thesame Re regime. In a body-centered coordinate system， the wingtiptraces a complex trajectory (Fig.5) in which it is not clear howuseful lift could be generated. In a ‘global’ coordinate system (i.e.one that translates with the animal but does not rotate) that therebyincludes the effect of body pitching， the pteropod effectively strokesits parapodia in a figure-of-eight pattern (Fig. 5). Figure-of-eightwingtip trajectories are common in flying insects (Ellington，1984a)and， when combined with a large angle of attack in both power and Fig.7.Angle between wings over time. Time variation of wing opening angleo during the fling phase of two consecutive power strokes of pteropod 3. Thesquares correspond to the stroke shown in Fig. 2. recovery strokes， have been shown to produce the most lift whencompared with other， insect-inspired wingtip trajectories (Lehmannand Pick， 2007). Limacina helicina uses a large angle of attack(46 deg in the power stroke and 49 deg in the recovery stroke)， atechnique that allows it to maximize lift. Furthermore， its strokeplanes for both power and recovery strokes lie approximately 29 degabove the horizontal plane. Drag on its appendages， acting parallelto the stroke plane， therefore provides additional upward verticalforce during both power and recovery strokes； this technique is alsoused by many insects (Wang，2004). Fig. 8. Flow fields during the end of the power stroke. Color contoursrepresent thex-component of vorticity. Vectors， which lie tangent in the plane，indicate flow direction and magnitude. The transverse plane shown is the sameas in Fig. 6. Fig.9. Flow fields during the recovery stroke. Color contours representthe x-component of vorticity. Vectors， which lie tangent in the plane， indicateflow direction and magnitude. The transverse plane， which bisects the shell atmid-recovery stroke， is 0.8 mm more anterior than that shown in Figs 6 and 8. Power stroke Separation of the parapodia at the beginning of the power strokedraws fluid downward into the growing， V-shaped gap between thewings (t'=0.18-0.22 in Fig. 6). The time variation of the angle obetween the wings during the fling is shown in Fig. 7. As theparapodia separate anteriorly to posteriorly， the downward flow alsohas an out-of-plane component. By t'=0.24， the flow has separatedfrom both wingtips to form elongated leading edge vortices， aprocess that continues att'=0.27. By t'=0.32 (Fig. 8)， these vorticeshave strengthened and are in the process of being shed from thewingtips. Shear layers at the base ofeach wing also begin to developas the pteropod rises through the leading edge vortices， pushing abow wave upward in front of the pteropod’s shell. This upwardsflow is pushed down along the pteropod’s wings by the now-shedleading edge vortices， creating an elongated region of high vorticityalong each wing (t’=0.35-0.37). At t'=0.37， the parapodia areapproaching the sides of the shell， and flow on the wing uppersurface continues to follow the wing down， at speeds up toapproximately 13 mm s. Maximum flow speeds reach 20 mm s-at t'=0.42 as the parapodia close along the sides of the shell， and thisflow continues to feed the leading edge vortex rings. The downwardimpulse of flow created by the power stroke is evident at t'=0.48 (onboth sides ofthe pteropod). A new pair of oppositely signed vorticesbeneath the pteropod is created by the interaction of these downwardpulses and the flow pulled upward beneath the pteropod shell. Byt'=0.52， the vortices， moving downward and away from thepteropod at an angle of approximately 45 deg relative to vertical，have separated from the shell and begun to decay. Flow fields detailing the recovery stroke are shown in Fig. 9. Thet'=0.52 time point is shown in both Figs 8 and 9 in order to illustratethe three-dimensional nature of the flow. In the posterior plane(Fig. 8)， the downward flow pulse created at the end of the powerstroke moves outward away from the pteropod. In Fig. 9， thedownward flow pulse moves more vertically downward and curvesback up underneath the pteropod， likely because the parapodiacomplete the power stroke by curling upward along the shell. Theshed leading edge vortices also are weaker and lower in the moreanterior plane. In addition， the vorticity patches bound to the pteropodbody in the anterior plane (Fig. 9) are not present in the posterior plane(Fig. 8). At t'=0.74， the downward flow along the sides of thepteropod resulting from the power stroke remains (and persiststhroughout the recovery stroke). The parapodia are well into therecovery stroke， and vorticity has formed on the parapodia’s upperleading edges. These vortices grow slightly but remain attached to thewings at t’=0.78. Byt’=0.85， these leading edge vortices havestrengthened and separated from the parapodia. Downward flow fromthe wingtips joins with the downward flow created by the powerstroke to strengthen the pre-existing vortices underneath theparapodia. Similar to the power stroke， the rising pteropod pushes abow wave ahead， which curves around and downward to create anelongated high vorticity region along the parapodia， a trend thatcontinues at t'=0.91. Also at t’=0.91， the shed leading edge vortex isstrengthened by the downward impulse from the recovery stroke.These vortices subsequently decay and translate away from thepteropod， as seen at t'=0.97， until， at the beginning of the next powerstroke， they resemble those vortices seen at t'=0.06 in Fig. 6. DISCUSSION Hyper-pitching Limacina helicina generates its figure-of-eight wingtip trajectory in aunique manner that has implications for micro aerial vehicle (MAV)design. Figure-of-eight wingtip trajectories seen in flying insects(Weis-Fogh， 1973) and shell-lessisgymnosomatous pteropods(Satterlie et al.， 1985； Borrell et al.，2005； Szymik and Satterlie，2011) are accomplished by active elevation of the wingtip inpreparation for the next half-stroke. In L.helicina， the figure-of-eightpattern is enabled by extreme rotation of the shell. This hyper-pitching of 50-60 deg elevates the wingtips at the end of eachhalf-stroke in preparation for the next half-stroke and accounts for25% and 51% of wing elevation at the beginning of the recovery andpower strokes， respectively. Limacina helicina’s round shell， with alow moment of inertia and low rotational drag， naturally facilitates thishyper-pitching whereas the elongated bodies of the gymnosomatouspteropods have a greater moment of inertia and greater rotational dragand thus experience correspondingly less body rotation (11 deg inClione antarctica) (Borrell et al.， 2005). Such extreme pitchingduring regular swimming or flying is rare， although Kiorboe et al.(2010) found body pitching up to 55 deg in a jumping Acartia tonsacopepod. Many insects fly with body angle oscillations of 3 deg orless (Ellington， 1984a). Body kinematics are difficult to measure inthe tiny insects flying in the same Re range as L. helicina， but high-speed videos show little variation in body angle with individualwingbeats for thrips (Santhanakrishnan et al.， 2014). In contrast，Dudley (1990) found a much larger range for butterflies， with somespecies attaining body angle oscillations of 49 deg. Indeed， Changand Yen (2012) compared the erratic flight of butterflies with theswimming of L. helicina and suggested that， like butterflies，pteropods may evade predators with their irregular trajectoriesbrought on by hyper-pitching. While pitching is typically avoided in flapping MAV design and typical insect flight because of theproblems it poses for vehicle or animal stability and control， L.helicina ‘flight’suggests the opposite paradigm and that hyper-pitching could be incorporated into future MAV designs to passivelyprovide aerodynamic benefits. However， difficulties in maintainingcontrol and stability and in gathering and integrating sensoryinformation while hyper-pitching need to be investigated further. Flexible clap-and-fling： lift augmentation by the Weis-Foghmechanism Similar to many small insect species， L. helicina uses a version ofthe Weis-Fogh clap-and-fling mechanism to generate lift during itspower stroke (Fig. 6). The flow generated by the Weis-Foghmechanism has not previously been measured in a freely flying orswimming animal despite being extensively studied for 40 years(Weis-Fogh， 1973； Lighthill， 1973； Maxworthy， 1979； Ellington，1984a，b； Spedding and Maxworthy， 1986； Dickinson et al.， 1999；Miller and Peskin， 2005； Lehmann et al.， 2005； Kolomenskiy et al.，2011). In the classic Weis-Fogh mechanism， the wings clap togetherat the end of the recovery stroke and subsequently rotate apart in thepower stroke， with the trailing edge serving as a ‘hinge’. Thegrowing， V-shaped gap draws in fluid， initiating leading edgevortices around each wing， thereby increasing circulation aroundboth wings and increasing lift (Weis-Fogh， 1973；Lighthill， 1973；Maxworthy，1979； Ellington， 1984a，b； Spedding and Maxworthy，1986； Dickinson et al.， 1999). As the pteropod’s wings only touch attheir tips and do not fully clap together at the end of the recoverystroke， however， tltheppteropod'swing motionss are bettercharacterized as a ‘near-fling’or‘touch-and-fling’ rather than aclap-and-fling. The flow fields captured here， with elongated leading edgevortices forming and eventually shedding， show qualitativeagreement with dynamically scaled laboratory experiments andwith simulations of insect flight at similar Re (Maxworthy， 1979；Spedding and Maxworthy， 1986； Miller and Peskin， 2005；Lehmann et al.， 2005； Kolomenskiy et al.，2011). However， thespatial extent of the leading edge vortices relative to the wing sizeappears larger in the dynamically scaled experiments than inthe current study (see Maxworthy， 1979). This observation mayhave important ecologicalconsequences， minimizinga‘hydrodynamic footprint’ while swimmingisisanimportantstrategy for zooplankton to avoid predators， which often detecttheir prey through flow disturbances (Yen， 2000； Kiorboe et al.，2014). The distance between the wings at the beginning of thepower stroke may affect the scale of these vortices and the liftaugmentation from the Weis-Fogh mechanism. A mid-span gap between the parapodia at the beginning of thepower stroke likely decreases lift augmentation from the Weis-Foghmechanism. This mid-span gap of approximately the shell width(~1 mm) results from lateral separation of the thick， fleshy wingbases and from wing curvature during the stroke. The center-to-center gap between the parapodia at their insertion point isapproximately 0.3 mm， and the wing thickness at the insertionpoint is approximately 0.2 mm. The gap width decreases towardsthe wingtips as the highly flexible parapodia curve inwards to meetat their tips. Thus， in contrast to many insect species， the wings ofL. helicina do not lie parallel along their span at the beginning ofthefling (Chang and Yen，2012). Lehmann et al. (2005) investigated theimportance of this gap between the wings in a dynamically scaledmodel of a fruit fly by varying the lateral separation between the winghinges and the angular distance between the wings at the beginningof the fling phase (a in this study). These authors found that Upstroke Stroke Animal Wing Swimming Wingbeat angle of Downstroke plane Sinking length Wing length chord speed trequency attack angle of attack angle speed Species Reference (mm) (mm) (mm) (mm s (Hz) Ree (deg) (deg) (deg) (mm s ) Clione Satterlie Up to 20 Can 4.5 100 1-3 Estimated NA NA 15-20 7-10 limacina et al. exceed 5 at 200 (1985) Syzmik and 3-7 3.4-7.7 3.3-7.8 Tethered 1.1-3.2 48-319 59-63 64-70 12-17 NA Satterlie (2011) Clione Borrell et al. 7-22 2.4-4.5 1.8-5.4 1-7 0.8-1.6 15-123 63-80 NA 19-32 NA antarctica (2005) Limacina Chang and 1-3.4 1-4 Variable 13-44 4.5-9.4 NA NA NA NA 5-45 helicina Yen (2012) Current 1.6-2 2.1-2.9 0.5-0.6 15-26 4.3-4.7 49-60 49 46 29 NA study increasing both of these parameters decreased the lift augmentationdue to clap-and-fling. Specifically， for minimum lateral separationand initially parallel wings (o=0 deg)， lift was enhanced 13.3%compared with a case with only one wing (i.e. no interaction betweenwings)， whereas it was enhanced only about 4% for a greater lateralseparation for the same initial o. In the case of L. helicina， wingseparation likely also decreases the lift generated by clap-and-flingby allowing inward flow from the wing edges， thereby decreasing thestrength and size of the leading edge vortices at the wingtips.However， the lateral wing separation of L. helicina allows thetouching wings to angle inward and form a ‘canopy'over its body. InLehmann et al. (2005)， this canopy effect (called a ‘negative angulardistance’) is modeled for the greater lateral separation and led to afurther increase in clap-and-fling lift augmentation to 9% (againcompared with a one-wing case). Thus， though the gap between thewings of L. helicina seems to decrease the hydrodynamic benefit ofthe Weis-Fogh mechanism， this may be somewhat offset because ofthe canopy effect. It should be noted that the canopy effect is notrepresented in Fig. 7(i.e. the minimum value of a is 0 deg) as onlyone point between the parapodia bases (point A) was tracked. The act of flinging apart closely apposed wings generates bothhigh lift and high drag forces. Using a 2D computational model，Miller and Peskin (2005) found substantial drag forces involved inrotating closely apposed wings apart during the fling. In addition，Santhanakrishnan et al. (2014) varied the initial gap betweenporous wings and found large increases in drag and only modestincreases in lift with more closely spaced wings. Thus， while themid-span gap between the wings of L. helicina at the beginning ofthe fling likely decreases lift， this gap also likely reduces drag onthe wings during the fling， thus lowering the force requirementson the animal. Furthermore， Miller and Peskin (2009) found thatadding flexibility to the wing reduced the drag forces whilemaintaining lift forces during the fling. Jones et al. (2015)similarly found that wing flexibility increased vertical forceproduction in a simulated， tilted wing stroke similar to that used byL. helicina. Thus， the highly flexible parapodia of L. helicina alsomay reduce drag while sustaining lift during the fling andthroughout the stroke. It is difficult to estimate the relative importance of the Weis-Fogh mechanism in enhancing lift for L. helicina. Lehmann et al.(2005) measured lift enhancements of up to 17% for theirdynamically scaled Drosophila model， but this augmentationdepended greatly on lateral and angular wing separation and other kinematic parameters (LehmannandPick， 2007). Lifaugmentation by the Weis-Fogh mechanism is also dependenton Reynolds number. The computational model of Miller andPeskin (2005) shows increased lift enhancement with decreasingRe， whereas the experimental results of Lehmann et al. (2005) donot show a clear trend. Limacina helicina operates at a lower Rethan Drosophila， but L. helicina may also use other unsteady flowtechniques to increase lift production. For example， Chang andYen (2012) suggested that the clap of the parapodia against theshell at the end of the power stroke could create thrust bysqueezing fluid downwards. Another possibility is that theparapodia peeling away from the shell at the beginning of therecovery stroke may generate lift. Occlusion by the shell andparapodianmake itdifficulttodetermineewhether thesemechanisms are present in the current case. Comparison with other planktonic gastropods It is interesting to compare L. helicina swimming with that of theshell-less pteropods Clione limacina and C. antarctica. As seen inTable 2， the shell sizes of L. helicina in the current study aresubstantially smaller than the body lengths of the gymnosomatouspteropods. The swimming speeds of L. helicina are slower thanthose of its predator C. limacina but faster than those ofC. antarctica. Accounting for body size， however， shows thatL. helicina， C. limacina and C. antarctica swim at maximumnormalized swimming speeds of approximately 13， 5 and 0.3 bodylengths s-， respectively. The slower swimming speeds ofC. antarctica perhaps may be partially explained by the higherviscosity of the cold， polar seawater. The wingbeat frequency ofL. helicina is also higher than those of the shell-less pteropods. Thefaster normalized swimming speed and greater beat frequency ofL. helicina indicate that it is a more agile swimmer than its predator，the shell-less C. limacina.The high beat frequency of L. helicina，coupled with its extreme pitching angle， should enable it tofrequently change swimming direction. The resulting tortuousswimming pathway may enable it to evade the larger， more slowlystroking C. limacina that depends on tail bending to changeswimming direction (Satterlie et al.， 1985). The shell of L. helicina also plays a large role in its swimmingbehavior. In addition to facilitating the hyper-pitching discussedabove， the shell’s weight obviously leads to a greater sinking speedfor L. helicina and a greater need for it to generate lift than for theshell-less pteropods. The shell also ensures that the swimming appendages of L. helicina have closely spaced insertion points， amorphological arrangement that allows this pteropod’s parapodia toclosely approach each other and perform the lift-enhancing Weis-Fogh maneuver. The appendages of the shell-less pteropods， incontrast， are located on opposite sides of its torpedo-shaped body andcannot approach each other along their length. Satterlie et al. (1985)posited that C. limacina peels its appendages away from its body in away that could create lift， but no flow measurements have beenperformed on Clione to investigate its lift generation mechanisms.Whereas we have shown that L. helicina mimics the lift-producingkinematics and fluid dynamics of insects， the fluid dynamics of theflow around the wings of the Clione species are essentially unknown.The outcomes among studies of Clione swimming are contradictory，with Satterlie et al. (1985) concluding that the wing movement of C.limacina produces lift in both upstroke and downstroke， Borrell et al.(2005) concluding that pteropods are poorly equipped to propel vialift forces， and Szymik and Satterlie (2011) concluding that C.limacina propulsion is provided by a combination of lift-based anddrag-based mechanisms. Flow measurements would be valuable inresolving this uncertainty. CONCLUSIONS Our measurements strongly indicate that L. helicina uniquelyemploys lift-based swimming instead of drag-based swimmingused by nearly all zooplankton. This pteropod ‘flies’underwaterby stroking its parapodia in a figure-of-eight trajectory at a highangle of attack with an inclined stroke plane in much the same waythat tiny insects such as thrips and fruit flies fly in air. The wingkinematic pattern is uniquely facilitated by L. helicina’s hyper-pitching， which also may aid in evasion of predators. Moreover，hyper-pitching offers an alternative vision for flapping MAVdesign. In accordance with most flying animals， pitchingtraditionally has been eschewed in favor of body stability， butL. helicina demonstrates that extreme pitching， when integratedwith wing kinematics， may offer passive aerodynamic benefits.Limacina helicina further earns its common name of ‘seabutterfly’by borrowing the Weis-Fogh mechanism from theinsect world as it performs a ‘near-fling’maneuver to augment liftgeneration during its power stroke. Though Gastropoda andInsecta diverged 550 million years ago， L. helicina and flyinginsects swimand fly， respectively， in similar physicalenvironments (at least in terms of the balance of inertial andviscous forces as quantified by Re) and employ similar wingkinematics and fluid dynamic lifftt generation mechanisms.Limacina helicina and tiny insects thus represent a remarkableevolutionary convergence of locomotion techniques employed bydissimilar animals that operate in a similar Re regime. Clionespecies and other planktonic gastropods， which， like L. helicina，are also fragile and difficult to study， may also use lift-basedlocomotion and ought to be further investigated. Acknowledgements We thank Anna Skipper for assistance in processing data. We thank Bill Petersonand Jay Peterson for collecting and sending the pteropods. Competing interests The authors declare no competing or financial interests. Author contributions J.Y. secured and cared for the pteropods. J.Y.， D.W.M. and D.R.W. designed thestudy. J.Y. and D.W.M. performed the experiments. D.W.M. and D.A. processed thetomographic PIV data for flow fields and kinematics. D.W.M.， D.R.W.， D.A. and J.Y.wrote the manuscript. All authors approved the final manuscript. Funding Funding was provided by U.S. National Science Foundation Grant PLR-1246296. Supplementary information Supplementary information available online at http：//jeb.biologists.org/lookup/suppl/doi：10.1242/jeb.129205/-/DC1 References ( Adhikari， D . and Longmire， E. K.(2012). Vi s ual hull method fo r tomographic PI Vm easurement of flow around mo v ing objects. Ex p . Fl u ids 53， 943-964. ) Bednarsek， N.，Tarling， G. A.， Fielding， S. and Bakker，D. C. E.(2012). Population ( dynamics a n d biogeochemical sig n ificance of Limacina helicina antarctica in the S cotia Sea ( Southern O cean). D eep Sea R e s. l/ T op Stud Oceanogr 59-60， 105-116. ) Borrell，B. J.，Goldbogen，J.A. and Dudley，R.(2005). Aquatic wing flapping at lowReynolds numbers： swimming kinematics of the Antarctic pteropod， Clioneantarctica. J. Exp. Biol. 208， 2939-2949 Chang， Y. and Yen， J. (2012). Swimming in the intermediate Reynolds range：kinematics of the pteropod Limacina helicina. Integr. Comp. Biol. 52， 597-615. Cooter， R. J. and Baker， P. S. (1977). Weis-Fogh clap and fling mechanism inLocusta. Nature 269，53-54. Dickinson， M. H. and Gotz， K. G. (1996). The wake dynamics and flight forces ofthe fruit fly Drosophila melanogaster. J. Exp.Biol. 199， 2085-2104. Dickinson， M. H.， Lehmann， F.-O. and Sane， S. P. (1999). Wing rotation and theaerodynamic basis of insect flight. Science 284， 1954-1960. Dudley， R. (1990). Biomechanics of flight in neotropical butterflies： morphometricsand kinematics. J. Exp. Biol. 150， 37-53. Ellington， C. P. (1984a). The aerodynamics of hovering insect flight.Ⅲ. Kinematics.Philos. Trans.R. Soc. B Biol. Sci.305，41-78. Ellington， C. P. (1984b). The aerodynamics of hovering insect flight. IV.Aerodynamic mechanisms. Philos. Trans.R. Soc. B Biol. Sci. 305， 79-113. Fuchiwaki， M.， Kuroki， T.， Tanaka， K. and Tababa，T.(2013).Dynamic behavior ofthe vortex ring formed on a butterfly wing. Exp. Fluids 54， 1450. Gilmer， R. W. and Harbison， G. R. (1986). Morphology and field behavior ofpteropod molluscs： feeding methods in the families Cavoliniidae， Limacinidae andPeraclididae (Gastropoda： Thecosomata). Mar. Biol. 91， 47-57. Hays， G. C. (2003). A review of the adaptive significance and ecosystemconsequences of zooplankton diel vertical migrations. In Migrations andDispersal of Marine Organisms (ed. M. B. Jones， A. Ingolfsson， E. Olafsson，G. V. Helgason， K. Gunnarsson and J. Svavarsson)， pp. 163-170. TheNetherlands： Kluwer Academic Publishers. Hedrick， T. L. (2008). Software techniques for two- and three-dimensional kinematicmeasurements of biological and biomimetic systems. Bioinspir. Biomim. 3，034001. Jones， S. K.，Laurenza， R.， Hedrick， T. L.， Griffith， B. E. and Miller，L. A. (2015). Lift vs. drag based mechanisms for vertical force production in the smallest flying. insects. J. Theor. Biol. 384， 105-120. Kiorboe，T.， Andersen， A.，Langlois， V. J. and Jakobsen， H. H.(2010). Unsteadymotion： Escape jumps in planktonic copepods， their kinematics and energetics.J. R. Soc. Interface 7， 1591-1602. Kiorboe， T.， Jiang， H.， Goncalves， R. J.， Nielsen， L. T. and Wadhwa，N. (2014).Flow disturbances generated by feeding and swimming zooplankton. Proc. Natl.Acad. Sci. USA 111， 11738-11743. Kolomenskiy， D.， Moffatt， H. K.， Farge， M. and Schneider， K. (2011). TheLighthill-Weis-Fogh clap-fling-sweep mechanism revisited. J. Fluid Mech. 676，572-606. Lehmann， F.-O. and Pick， S. (2007). The aerodynamic benefit of wing-winginteraction depends on stroke trajectory in flapping insect wings. J. Exp. Biol.210，1362-1377. Lehmann， F.-O.，Sane， S. and Dickinson， M. (2005). The aerodynamic effectsof wing-wing interaction in flapping insect wings. J. Exp. Biol. 208，3075-3092. Lighthill， M. J. (1973). On the Weis-Fogh mechanism of lift generation. J. FluidMech. 60，1-17. Maxworthy，T. (1979). Experiments on the Weis-Fogh mechanism of lift generationby insects in hovering flight. Part 1. Dynamics of the ‘fling’. J. Fluid Mech. 93，47-63. McGhee， G. (2011). Convergent Evolution. Cambridge， MA： MIT Press.Miller， L. A. and Peskin， C. S. (2005). A computational fluid dynamics of'clap andfling’in the smallest insects. J. Exp. Biol. 208， 195-212. Miller， L. A. and Peskin， C. S. (2009). Flexible clap and fling in tiny insect flight.J. Exp. Biol. 212，3076-3090. Murphy，D. W.，Webster， D. R. and Yen， J.(2012).A high-speed tomographic PIVsystem for measuring zooplanktonic flow. Limnol. Oceanogr. Methods 10，1096-1112. Murphy，D. W.， Webster， D. R. and Yen，J.(2013). The hydrodynamics of hoveringin Antarctic krill. Limnol. Oceanogr. Fluids Environ. 3，240-255. Santhanakrishnan， A.， Robinson， A. K.， Jones， S.，Low， A. A.， Gadi， S.， Hedrick， T. L. and Miller， L. A. (2014). Clap and fling mechanism with interacting porouswings in tiny insect flight. J. Exp. Biol. 217， 3898-3909. Satterlie， R. A.，LaBarbera，M. and Spencer，A. N.(1985). Swimming in the pteropodmollusk Clione limacina. 1. Behaviour and morphology. J. Exp. Biol. 116， 189-204. Spedding， G. R. and Maxworthy，T.(1986). The generation of circulation and lift ina rigid two-dimensional fling. J. Fluid Mech. 165，247-272. Strickler，R.(1975). Swimming of planktonic Cyclops species (Copepoda， Crustacea)：pattern， movements and their control. In Swimming and Flying in Nature， Vol.2. (ed.T. Wu， C. Brokaw and C. Brennen)， pp.599-613. New York： Plenum Press. Szymik， B. G. and Satterlie， R. A. (2011). Changes in wingstroke kinematicsassociated with a change in swimming speed in a pteropod mollusk， Clionelimacina. J. Exp. Biol. 214， 3935-3947. Valentine，J.W.(1997).Cleavage patterns and the topology of the metazoan tree oflife. Proc. Natl. Acad. Sci. USA 94， 8001-8005. Vogel， S. (1967). Flight in Drosophila Il： variations in stroke parameters and wingcontour. J. Exp. Biol.46， 383-392. Walker， J. A. and Westneat， M. W. (2000). Mechanical performance of aquaticrowing and flying. Proc. R. Soc. B Biol. Sci.. 267，1875-1881. Wang，Z. J.(2004). The role of drag in insect hovering. J.Exp.Biol. 207， 4147-4155.Weis-Fogh， T.(1973). Quick estimates of flight fitness in hovering animals， includingnovel mechanisms for lift production. J. Exp. Biol. 59，169-230. Weis-Fogh， T. (1975). Unusual mechanisms for the generation of lift in flyinganimals. Sci. Am. 233， 80-87. Yen，J. (2000). Life in transition： balancing inertial and viscous forces by planktoniccopepods. Biol. Bull. 198， 213-224. Received July Accepted December In a remarkable example of convergent evolution, we show that thezooplanktonic sea butterfly Limacina helicina ‘flies’ underwater in thesameway that very small insects fly in the air. Both sea butterflies andflying insects stroke their wings in a characteristic figure-of-eightpattern to produce lift, and both generate extra lift by peeling theirwings apart at the beginning of the power stroke (the well-knownWeis-Fogh ‘clap-and-fling’ mechanism). It is highly surprising to find azooplankter ‘mimicking’ insect flight as almost all zooplankton swim inthis intermediate Reynolds number range (Re=10–100) by using theirappendages as paddles rather than wings. The sea butterfly is alsounique in that it accomplishes its insect-like figure-of-eight wing strokeby extreme rotation of its body (what we call ‘hyper-pitching’), aparadigm that has implications for micro aerial vehicle (MAV) design.No other animal, to our knowledge, pitches to this extent under normallocomotion.KEY WORDS: Pteropods, Zooplankton, Swimming, Weis-Foghmechanism, Insect flight, Convergent evolution