高雷诺数湍流中惯性粒子团聚检测方案(激光干涉仪)

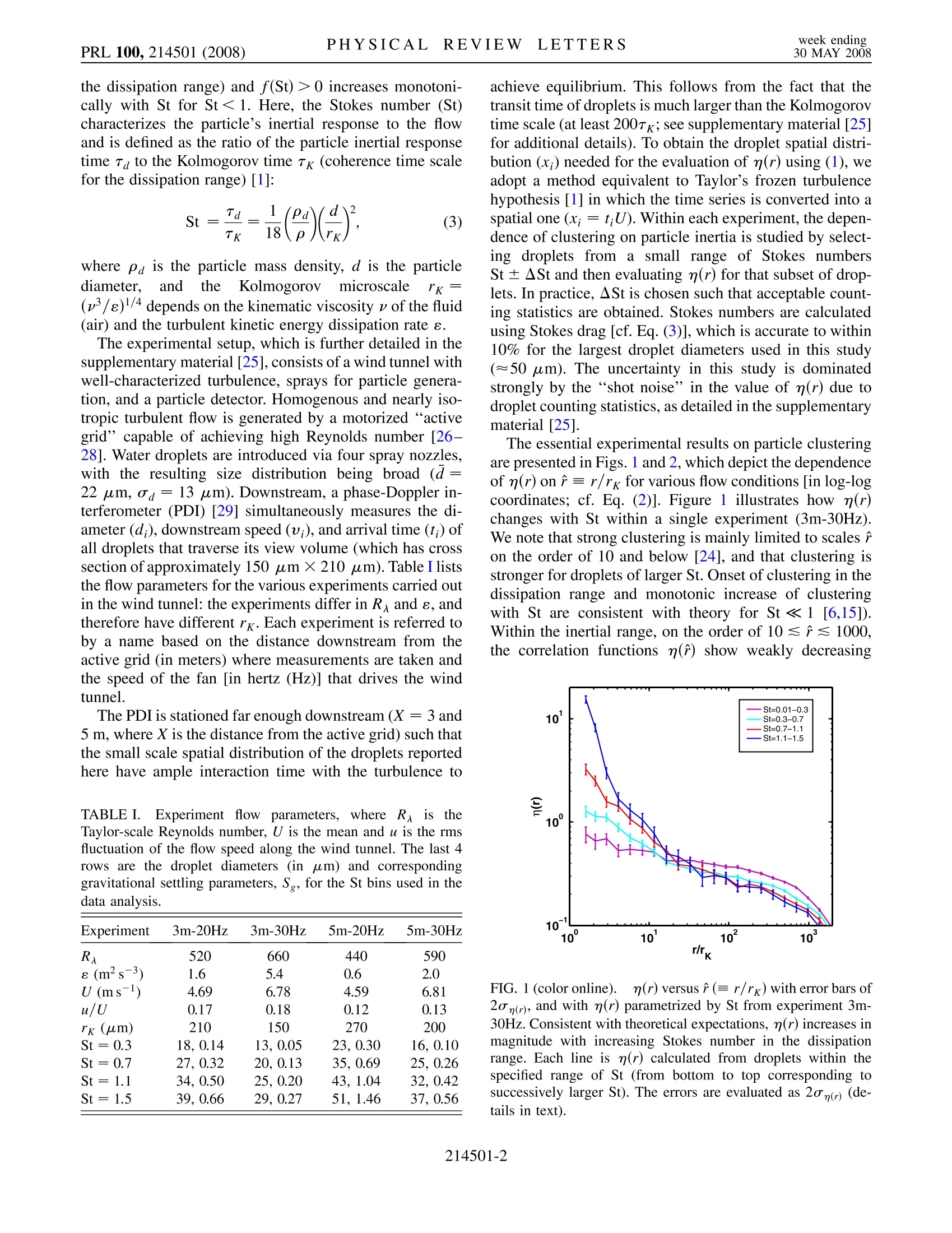
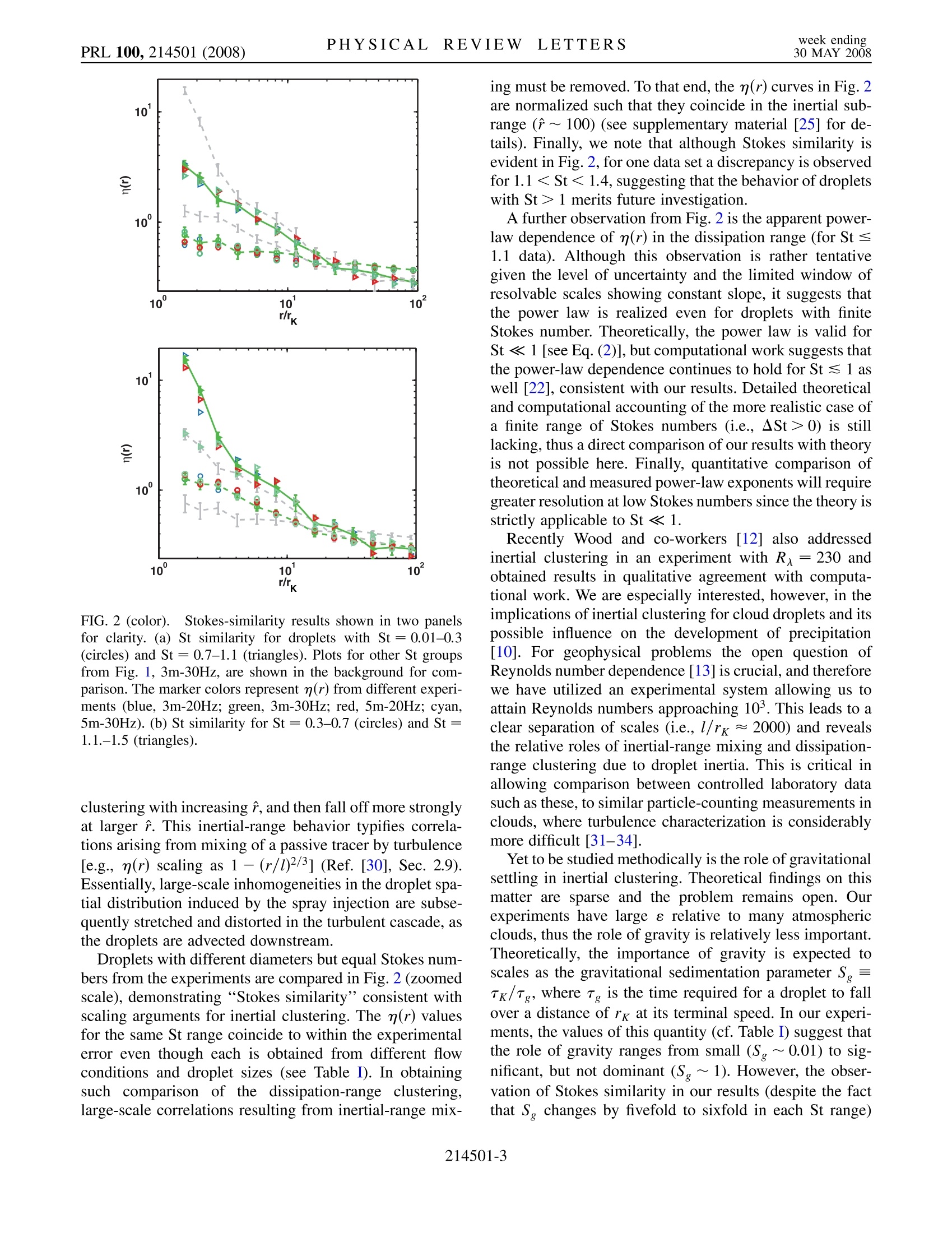
ResearchGateSEE PROFILE PHYSICAL REVIEW LETTERSweek ending30 MAY 2008PRL 100，214501(2008) See discussions，stats， and author profiles for this publication at： https：//www.researchgate.net/publication/51395307 Inertial Clustering of Particles in High-Reynolds-Number Turbulence Article in Physical Review Letters · May 2008 DOI： 10.1103/PhysRevLett.100.214501·Source： PubMed CITATIONS79 READS 122 5 authors，including： Ewe Wei SawSun Yat-Sen University (Zhuhai) Patrick Chuang University of California， Santa Cruz 28 PUBLICATIONS 366 CITATIONS 100 PUBLICATIONS 2，435 CITATIONS SEE PROFILE Armann Gylfason Reykjavik University 26 PUBLICATIONS 324 CITATIONS SEE PROFILE Some of the authors of this publication are also working on these related projects： Project Singularities in navier-stokes View project Project Dissipation and Transport Taylor-Couette，Rayleigh-Benard and von Karman View project Allcontent following this page was uploaded by Armann Gylfason on 27 May 2014. The user has requested enhancement of the downloaded file. Inertial Clustering of Particles in High-Reynolds-Number Turbulence Ewe Wei Saw， Raymond A. Shaw， * Sathyanarayana Ayyalasomayajula，Patrick Y. Chuang， and Armann Gylfason+International Collaboration for Turbulence Research and Department of Physics， Michigan Technological University， Houghton， Michigan 49931， USA International Collaboration for Turbulence Research and Sibley School of Mechanical and Aerospace Engineering， Cornell University， Ithaca， New York 14853， USA Department of Earth Sciences， University of California Santa Cruz， Santa Cruz， California 95064， USA(Received 15 August 2006； published 28 May 2008) We report experimental evidence of spatial clustering of dense particles in homogenous， isotropicturbulence at high Reynolds numbers. The dissipation-scale clustering becomes stronger as the Stokesnumber increases and is found to exhibit similarity with respect to the droplet Stokes number over a rangeof experimental conditions (particle diameter and turbulent energy dissipation rate). These findings are inqualitative agreement with recent theoretical and computational studies of inertial particle clustering inturbulence. Because of the large Reynolds numbers a broad scaling range of particle clustering due toturbulent mixing is present， and the inertial clustering can clearly be distinguished from that due to mixingof fluid particles. DOI： 10.1103/PhysRevLett.100.214501 PACS numbers： 47.55.-t， 47.27.Gs， 47.27.Jv， 92.60.Nv It is a common observation that a “passive”tracerinjected nonuniformly into a turbulent flow (e.g.， a sub-stance that only marks but does not modify the flow， suchas smoke in air or milk in tea) will soon be stirred andmixed by the random vortices in the turbulence until itattains a uniform distribution. Such high mixing power isin fact a hallmark of turbulent flow [1]. One might reason-ably ask if the same holds true when the substance is nolonger a perfect fluid tracer， such as one that consists ofmacroscopically discrete particles possessing finite inertia，like the distribution of water droplets in turbulent clouds(e.g.， actively convective cumulus clouds). In fact， waterdroplets with mass density 10° times greater than that of airare dynamically stubborn and do not exactly follow themotion of the host fluid. As a result， these “inertial parti-cles” should have a steady state spatial distribution differ-ing from that of a uniform field of fluid particles [2-7]. The inertial clustering phenomenon has implications fora wide range of problems in nonlinear and fluid dynamics，including the formation of rain by droplet collisions inatmospheric clouds [8-10]. Because the droplet collisionrate is proportional to droplet density squared， spatialcorrelations due to inertial clustering can result in accel-erated rain formation. Considerable progress has beenmade in computational and theoretical studies of inertialclustering， but experimental results are sparse [11，12] andthe nature of inertial clustering at high Reynolds numbersremains an open problem [13]. Qualitatively， inertial clus-tering can be understood as the result of particles beingcentrifuged out of turbulent vortices and thus congregatingin regions of high strain [3，5]. Turbulence is a multiscaleprocess in which energy injected at large scales (of order l)"cascades”to progressively smaller scales through non-linear interactions such as vortex stretching. Over most ofthese spatial scales， known as the inertial range， fluid inertia dominates over viscous forces； the scales at whichviscosity becomes important lie in the dissipation range.The clustering of inertial particles is significant at dis-sipation scales and below because it is in this range thatturbulent vorticity andaccelerations arestrongest[9，14，15]. It should be noted， however， that alternate inter-pretations and approaches exist [16-20]， adding impetusto the need for experimental data capable of elucidatingmechanisms and constraining theory. To that end， it is thepurpose of this Letter to describe an experimental study ofinertial clustering and its dependence on particle size andturbulence conditions at high Reynolds numbers. Suitable quantification of clustering is provided by theparticle pair correlation function n(r) [5，10]， whose mag-nitude characterizes the strength of clustering at scale r.Intuition on the properties of n(r) can be gained by exam-ining how it is calculated in our experiment for one-dimensional sampling of the particle spatial distribution[21]： where @(r) is the number of particle pairs separated by adistance within [r- 8r/2， r+8r/2]， Q is the total num-ber particle pairs in the sample， L is the sample length.Previous theoretical and direct-numerical-simulation stud-ies [6，9，15，22，23] suggest that under ideal conditions (ho-mogenous and isotropic turbulence， single-size particlepopulation， particle-fluid coupling following Stokes’slaw， dilute particle loading，and negligible role of gravity)n(r) satisfies a simple power law [24]： where rg is the Kolmogorov length scale (characterizing the dissipation range) and f(St)>0 increases monotoni-cally with St for St<1. Here， the Stokes number (St)characterizes the particle’s inertial response to the flowand is defined as the ratio of the particle inertial responsetime Ta to the Kolmogorov time Tk (coherence time scalefor the dissipation range) [1]： where pa is the particle mass density， d is the particlediameter.andtthe Kolmogorov imicroscale rk =(v/e)1/4 depends on the kinematic viscosity v of the fluid(air) and the turbulent kinetic energy dissipation rate e. The experimental setup， which is further detailed in thesupplementary material [25]，consists of a wind tunnel withwell-characterized turbulence， sprays for particle genera-tion， and a particle detector. Homogenous and nearly iso-tropic turbulent flow is generated by a motorized“activegrid”capable of achieving high Reynolds number [26-28]. Water droplets are introduced via four spray nozzles，with the resulting size distribution being broad (d=22 um， od=13 um). Downstream， a phase-Doppler in-terferometer (PDI) [29] simultaneously measures the di-ameter (d；)， downstream speed (u；)， and arrival time (t；) ofall droplets that traverse its view volume (which has crosssection of approximately150 um×210 um). Table I liststhe flow parameters for the various experiments carried outin the wind tunnel： the experiments differ in R and e， andtherefore have different rg. Each experiment is referred toby a name based on the distance downstream from theactive grid (in meters) where measurements are taken andthe speed of the fan [in hertz (Hz)] that drives the windtunnel. The PDI is stationed far enough downstream (X=3 and5m， where X is the distance from the active grid) such thatthe small scale spatial distribution of the droplets reportedhere have ample interaction time with the turbulence to TABLE I. Experiment flow parameters，where Ris theTaylor-scale Reynolds number， U is the mean and u is the rmsfluctuation of the flow speed along the wind tunnel. The last 4rows are the droplet diameters (in um) and correspondinggravitational settling parameters， Sg， for the St bins used in thedata analysis. Experiment 3m-20Hz 3m-30Hz 5m-20Hz 5m-30Hz R 520 660 440 590 e (m²s-3) 1.6 5.4 0.6 2.0 U (ms-) 4.69 6.78 4.59 6.81 u/U 0.17 0.18 0.12 0.13 rk (um) 210 150 270 200 St=0.3 18，0.14 13，0.05 23，0.30 16， 0.10 St=0.7 27，0.32 20，0.13 35，0.69 25， 0.26 St=1.1 34，0.50 25，0.20 43，1.04 32，0.42 St=1.5 39，0.66 29，0.27 51，1.46 37，0.56 achieve equilibrium. This follows from the fact that thetransit time of droplets is much larger than the Kolmogorovtime scale (at least 200Tx； see supplementary material [25]for additional details). To obtain the droplet spatial distri-bution (x；) needed for the evaluation of n(r) using (1)， weadopt a method equivalent to Taylor’s frozen turbulencehypothesis [1] in which the time series is converted into aspatial one (x；=t；U). Within each experiment， the depen-dence of clustering on particle inertia is studied by select-ing droplets from a small range of Stokes numbersSt ±ASt and then evaluating n(r) for that subset of drop-lets. In practice， ASt is chosen such that acceptable count-ing statistics are obtained. Stokes numbers are calculatedusing Stokes drag [cf. Eq. (3)]， which is accurate to within10% for the largest droplet diameters used in this study(≈50 um). The uncertainty in this study is dominatedstrongly by the “shot noise”in the value of n(r) due todroplet counting statistics， as detailed in the supplementarymaterial[25]. The essential experimental results on particle clusteringare presented in Figs. 1 and2， which depict the dependenceof n(r) on ?=r/rx for various flow conditions [in log-logcoordinates； cf. Eq.(2)]. Figure 1 illustrates how n(r)changes with St within a single experiment (3m-30Hz).We note that strong clustering is mainly limited to scales ron the order of 10 and below [24]， and that clustering isstronger for droplets of larger St. Onset of clustering in thedissipation range and monotonic increase of clusteringwith St are consistent with theory for St <1 [6，15]).Within the inertial range， on the order of 10 ≤1≤1000，the correlation functions n(r) show weakly decreasing k FIG. 1 (color online). n(r) versus r(=r/rk) with error bars of2o(r)， and with n(r) parametrized by St from experiment 3m-30Hz. Consistent with theoretical expectations， n(r) increases inmagnitude with increasing Stokes number in the dissipationrange. Each line is n(r) calculated from droplets within thespecified range of St (from bottom to top corresponding tosuccessively larger St). The errors are evaluated as 2o n(r) (de-tails in text). rrk FIG. 2 (color).Stokes-similarity results shown in two panelsfor clarity. (a) St similarity for droplets with St=0.01-0.3(circles) and St= 0.7-1.1 (triangles). Plots for other St groupsfrom Fig. 1， 3m-30Hz， are shown in the background for com-parison. The marker colors represent n(r) from different experi-ments (blue， 3m-20Hz； green， 3m-30Hz； red， 5m-20Hz； cyan，5m-30Hz). (b) St similarity for St = 0.3-0.7 (circles) and St =1.1.-1.5 (triangles). clustering with increasing r， and then fall off more stronglyat larger r. This inertial-range behavior typifies correla-tions arising from mixing of a passive tracer by turbulence[e.g.， n(r) scaling as 1- (r/l)2/3] (Ref. [30]， Sec. 2.9).Essentially， large-scale inhomogeneities in the droplet spa-tial distribution induced by the spray injection are subse-quently stretched and distorted in the turbulent cascade， asthe droplets are advected downstream. Droplets with different diameters but equal Stokes num-bers from the experiments are compared in Fig. 2 (zoomedscale)， demonstrating “Stokes similarity”consistent withscaling arguments for inertial clustering. The n(r) valuesfor the same St range coincide to within the experimentalerror even though each is obtained from different flowconditions and droplet sizes (see Table I). In obtainingsuch comparison of the dissipation-range clustering，large-scale correlations resulting from inertial-range mix- ing must be removed. To that end， the n(r) curves in Fig. 2are normalized such that they coincide in the inertial sub-range (?~100) (see supplementary material [25] for de-tails). Finally， we note that although Stokes similarity isevident in Fig. 2， for one data set a discrepancy is observedfor 1.1 < St <1.4， suggesting that the behavior of dropletswith St> 1 merits future investigation. A further observation from Fig. 2 is the apparent power-law dependence of n(r) in the dissipation range (for St ≤1.1 data). Although this observation is rather tentativegiven the level of uncertainty and the limited window ofresolvable scales showing constant slope， it suggests thatthe power law is realized even for droplets with finiteStokes number. Theoretically， the power law is valid forSt <1 [see Eq. (2)]， but computational work suggests thatthe power-law dependence continues to hold for St ≤1 aswell [22]， consistent with our results. Detailed theoreticaland computational accounting of the more realistic case ofa finite range of Stokes numbers (i.e.， ASt >0) is stilllacking， thus a direct comparison of our results with theoryis not possible here. Finally， quantitative comparison oftheoretical and measured power-law exponents will requiregreater resolution at low Stokes numbers since the theory isstrictly applicable to St <1. Recently Wood and co-workers [12] also addressedinertial clustering in an experiment with Rx=230 andobtained results in qualitative agreement with computa-tional work. We are especially interested， however， in theimplications of inertial clustering for cloud droplets and itspossible influence on the development of precipitation[10]. For geophysical problems the open question ofReynolds number dependence [13] is crucial， and thereforewe have utilized an experimental system allowing us toattain Reynolds numbers approaching 10. This leads to aclear separation of scales (i.e.， l/rx ≈2000) and revealsthe relative roles of inertial-range mixing and dissipation-range clustering due to droplet inertia. This is critical inallowing comparison between controlled laboratory datasuch as these， to similar particle-counting measurements inclouds， where turbulence characterization is considerablymore difficult [31-34]. Yet to be studied methodically is the role of gravitationalsettling in inertial clustering. Theoretical findings on thismatter are sparse and the problem remains open. Ourexperiments have large e relative to many atmosphericclouds， thus the role of gravity is relatively less important.Theoretically， the importance of gravity is expected toscales as the gravitational sedimentation parameter S=Tk/T， where T is the time required for a droplet to fallover a distance ofrg at its terminal speed. In our experi-ments， the values of this quantity (cf. Table I) suggest thatthe role of gravity ranges from small (Sg~0.01) to sig-nificant， but not dominant (Sg~1). However， the obser-vation of Stokes similarity in our results (despite the factthat S， changes by fivefold to sixfold in each St range) suggests that the role of gravity in this work is limitedrelative to that of turbulence for the range of conditionsconsidered. The experiments described here provide support for theinertial clustering mechanism， and are in qualitative agree-ment with theoretical predictions. Clustering distinct fromthat expected for mixing of fluid particles is observed atdissipative scales， where fluid acceleration and vorticityreach a maximum. The magnitude of the clustering in-creases monotonically with droplet St， for St ≤ 1， whereSt is a parameter characterizing coupling between particlesand the fluid. Finally， under distinct flow conditions andwith varying droplet sizes， the dissipation-range clusteringis observed to exhibit Stokes similarity. This work was ·NSF((supported by the NSF (Grants No.ATM-0320953 and No.ATM-0535488) and by the Max PlanckInstitute for Dynamics and Self-Organization. We areindebted to E. Bodenschatz， L. Collins， J. Fugal，A. Kostinski， M. Larsen， E. Ochshorn， M. Stepanov，E. Variano， and Z. Warhaft for insightful comments andsuggestions. We thank J. Small， W. Bachalo， and the staffat Artium Technologies for technical assistance with thePDI instrument， and E.A. Cowen for the use of theDeFrees tunnel. ( * C o rresponding author. ) ( rashaw @mtu.edu ) ( ' Current address： School of Science and E ngineering，Reykjavik University， Reykjavik， Iceland. ) ( [1] H . Tennekes a nd J .L. L umley， A i First Course i in Turbulence (MIT， Cambridge， MA， 1 9 72). ) ( [2 ] M.R. Maxey， J. Fluid Mech. 174， 441 (1987). ) ( [3] . J . K. Eaton a nd J. R. F essler， Int. J. Multiphase Flow 20，169 (1994). ) ( [4] T . E lperin， N. Kleeorin， and I. Rogachevskii， Phys. Rev. Lett. 77，5373 (1996). ) ( [5 ] S . S undaram a n d L . R. Collins， J. F luid Mech. 3 35， 7 5 (1997). ) ( [6] E . B alkovsky， G . F alkovich， and A. Fouxon， P hys. R ev. Lett. 86，2790 (2001). ) ( [7] M 1 . Cencini， J. B ec， L. Biferale， G. B offetta， A. Celani，A. L anotte， S. M usacchio， an d F. T oschi， J. Tu r bul. 7， 1 (2006). ) ( [8 ] M . Pinsky a n d A. K h ain， Q. J. R. Meteorol. Soc. 123， 165 (1997). ) ( [9] G. Falkovich， A. Fouxon， and M. G. Stepanov， Nature(London) 419， 1 51 ( 2002). ) ( [10 ] R . A. Shaw， Annu. Rev. Fluid Mech. 35， 1 83(2003). ) ( [11] A . A liseda， A . Cartellier， F. Hainaux， and J.C. Lasheras， J. Fluid Mech. 468， 77 (2002). ) ( [12 ] A.M. Wood， W. Hwang， a nd J .K. Eaton， Int. J . M ultiphase Flow 3 1， 1220 ( 2005). ) ( [13 ] L .R . Collins and A. Keswani， Ne w J. Phys. 6， 11 9 (2 0 04). ) ( [14] L.P. Wang a nd M .R. M a xey， J . F l uid M ech. 256， 27(1993). ) ( [ 1 5] J. Chun， D. L. K och， S. L. R ani， A . Ahluwalia， a n d L.R. Collins， J. Fluid Mech. 536， 219 ( 2005). ) ( [16] K. Duncan， B. Mehlig， S. Ostlund， and M. Wilkinson， Phys. R ev. Lett. 95， 240602 ( 2 005). ) ( [17]T . Elperin， N. Kleeorin， V. S. L ’vov， I. Rogachevskii， and D. S okoloff， Phys. R ev. E 66， 0 36302 (2002). ) ( [18] L L. I. Zaichik and V.M. Alipchenkov， Phys. F l uids 15， 1776(2003). ) ( [19] S. Ghosh， J . D avila， J.C.R. Hunt， A. S r dic， H.J.S.Fernando， and P .R. J onas， Proc. R. Soc. A 4 61， 3059(2005). ) ( [20] L L . Chen， S. Goto， and J. C. Vassilicos， J. Fluid Mech. 553， 143 (2006). ) ( [21] G. L. H oltzer and L . R. Collins， J . Fluid M e ch. 45 9 ， 93 (2002). ) ( [22] W. C. R eade and L . R. Collins， P hys. F luids 12， 2 530(2000). ) ( [23] A. R. Kerstein a n d S.K. K r u eger， P h ys. Rev. E 7 3， 025302(R)(2006). ) ( [24] While it is usually stated that the theories apply to the limit r/rx<1， in fact th e po w er-law for m is p re d icted to continue t o the c o rrelation s c ale of ve l ocity gr a dients. That scale is on the order of r/r k ~10； see A. S. Monin and l A. M. Yaglom， Statistical Fluid ! Mechanics： Mechanics o f Turbulence (MIT， Cambridge， M A， 1 9 75)，Vol. II， Sec. 23.4 and Fig. 77； S. G. Saddoughi and S .V. Veeravalli， J. Fluid Mech. 268，3 3 3(1994)， Sec. 3.2.1 an d Fig. 10. ) ( [25] See EPAPS D ocument No.E - PRLTAO-100-039820 fo r details on the experimental s etup， error a nalysis， and t he data processing. For more informatio n on EPAPS， seehttp：//www.aip.org/pubservs/epaps.html. ) ( [26] SS. A yyalasomayajula， A . Gylfason， L.R. Co l lins， E. Bodenschatz， and Z. W arhaft， Phys. Rev. Le tt. 97， 144507 ( 2006). ) ( [27] L L . Mydlarski a nd Z. W a rhaft， J . Fluid Mech. 320， 331 (1996). ) ( [28] L L . Mydlarski a nd Z . W arhaft， J . Fluid Mech. 3 58， 1 35(1998). ) ( [29] P . Y. Chuang， E. W. S aw， J . D. Small， R. A. Shaw， C. M. Sipperley， G. A. Payne， and W.D. B achalo， Ae rosol Sci. T echnol. (to be published). ) ( [30] J.L. Lumley and H .A. P anofsky， T he S tructure ofAtmospheric Turbulence (John Wiley & Sons， New Yor k ，1964). ) ( [31] J .-L. Brenguier， T . Bourrianne， A . de Araujo Co e lho， J. Isbert ， R . Peytavi， D. Trevarin， and P. W eschler， J. Atmos.Ocean. Technol. 15， 1077 ( 1998). ) ( [32] A A. B. Kostinski and R. A. Shaw， J . Fluid Mech. 434， 3 8 9 (2001). ) ( [33] K. Lehmann， H. Siebert， M. Wendisch， and R. A. Shaw， Tellus， Ser . B 59 ， 57(2007). ) ( [34] M. P insky a nd A . Khain， J . Appl. M e teorol. 42， 6 5 (2003). ) /The American Physical Society We report experimental evidence of spatial clustering of dense particles in homogenous, isotropicturbulence at high Reynolds numbers. The dissipation-scale clustering becomes stronger as the Stokesnumber increases and is found to exhibit similarity with respect to the droplet Stokes number over a rangeof experimental conditions (particle diameter and turbulent energy dissipation rate). These findings are inqualitative agreement with recent theoretical and computational studies of inertial particle clustering inturbulence. Because of the large Reynolds numbers a broad scaling range of particle clustering due toturbulent mixing is present, and the inertial clustering can clearly be distinguished from that due to mixingof fluid particles.